Study on the life cycle of stars and their classification

Note: Before reading this article, it is important to understand the composition of matter and the nuclear fusion. You can find an article on "the composition of matter" and another on "nuclear reactions" on MH info. Unfortunately, those articles are not available in English.

How does a star form?

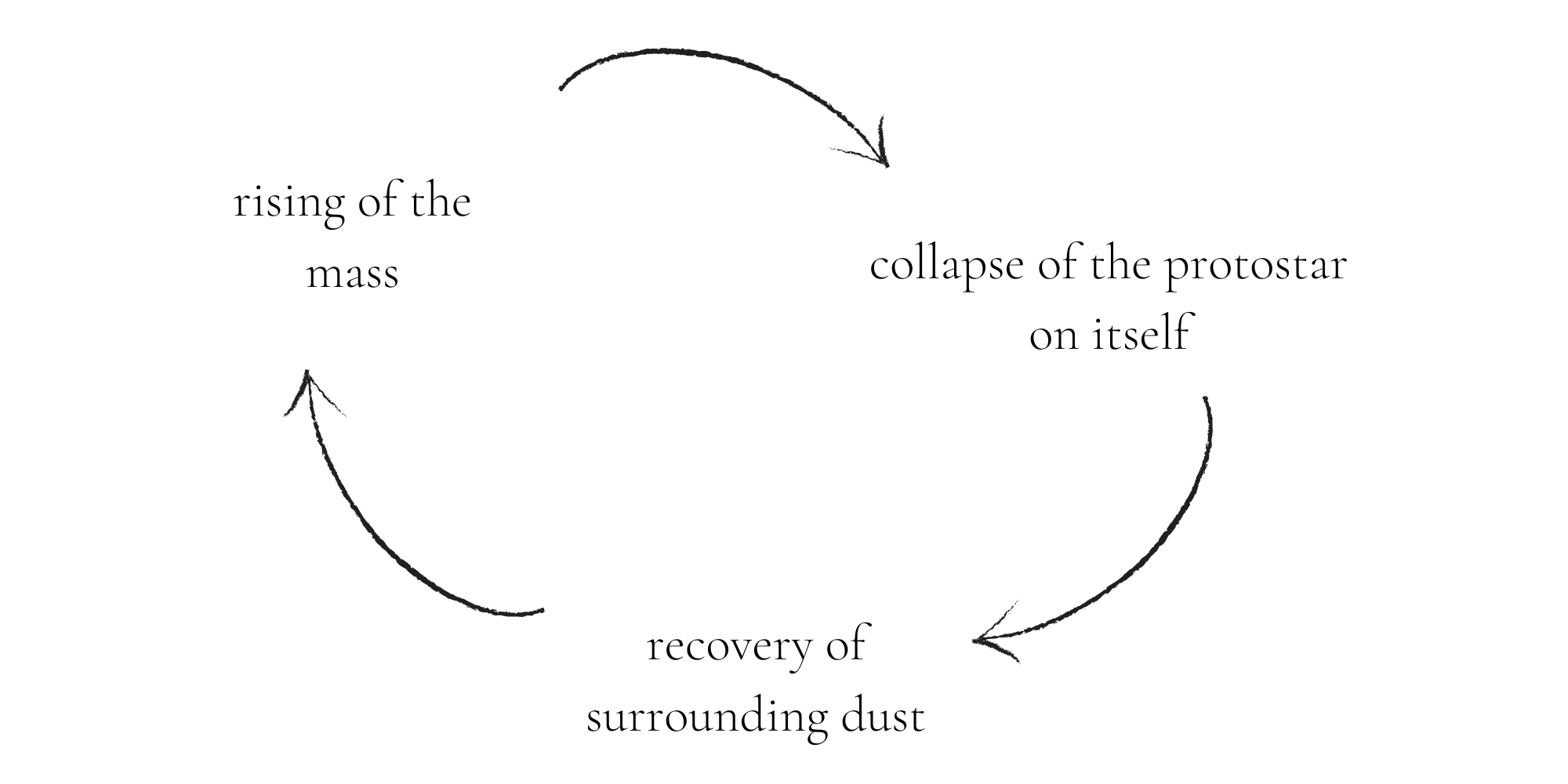
A star is formed in huge gas clouds made up largely of hydrogen (\( 1 \ p^+ + 1 \ e^- \)), which can measure tens of light years. These gigantic clouds of hydrogen emanate from supernovas (explosions of stars at the end of their lives), and the stars at the origin of these supernovas come from gas clouds. This implies that each star comes from another dead star (isn't that extraordinarily wonderful?)! These gas clouds are infinitesimally dense (a few tens of atoms/cm³, compared to the Earth, about 5x10¹⁹ , that is to say more than 50 billion billion atoms/cm³ ) and extend over astronomical lengths (a pun that is totally unintentional). Knowing that the only force they are subject to is their own gravity, the atoms attract each other, and the cloud progressively becomes denser: the cloud is said to collapse on itself. As the gravitational attraction is extremely weak (the gravitational interaction is the weakest fundamental interaction) this takes place over millions of years. When the density of the cloud is high enough, the hydrogen atoms combine to form dihydrogen molecules (chemical transformation). These are now molecular clouds.

© MH info Formation of a protostar

© NASA The Eagle Nebula

The denser the cloud is, the higher the pressure and temperature are. From 3 000 °C the dihydrogen molecules split into hydrogen atoms, and between 6 000 and 10 000 °C the atoms are ionized, forming a plasma. The collapse of the gas cloud can take hundreds of thousands of years, and the star does not yet shine (it is called a protostar). When the temperature reaches about 10 million degrees, nuclear fusion reactions can start (see nuclear reactions article ; this article is not available in English), and the star can now start to shine.

The Vogt-Russel theorem, established by Heinrich Vogt and Henry Norris Russell, states that their further evolution will be entirely determined by their mass. Although it has never been formally proven, it is still considered a theorem. The chemical composition of stars can, however, influence the nuclear fusion mechanism used by the star. We can also talk about metallicity, the fraction of its mass that is not hydrogen or helium.

How does fusion take place in the core of the stars?

Since then begin the essential phase of each star, the main sequence. This is the longest period of a star's life, as the name suggests. During this entire period, the star fuses its hydrogen.

Stellar fusion is slightly different from the one of an H-bomb or the kind of fusion reactions we would like to trigger in a nuclear fusion power plant, including the ITER project on Earth. As it is said in the article on nuclear reactions, quantum tunnelling occurs about once in every 100 million (10^-8 ) collisions. In a star like the Sun, a proton undergoes about 2 billion billion collisions/second (10¹⁵ /s). So, every second, quantum tunnelling can occur about 20 million times (2 x 10¹⁵ x 10^-8 = 20 millions).

Fusion can only occur in the core of the star, the area with the highest temperature of the star, representing only a few percent of its volume but all the same 30% of its mass. The temperature is around 15 million Kelvin and the pressure around 26 petapascals (in a star like the Sun), that is to say around 70 000 times higher than in the Earth's core. By way of comparison, we can fit 2 million times more hydrogen atoms into 1 m² of solar core than we can on Earth.

A proton can be transformed into a neutron by radioactivity \(\beta^+\) because of the weak nuclear interaction with a probability of one out of 10²⁴ (1 million billion billion). To be exact, this transformation is the apparent consequence of another transformation: one of the proton's down quarks interacts with the weak field and decays into a neutron and a W⁺ boson, which decays into a positron and neutrino.

The most common chain is the proton-proton chain, or PP chain (PP1 in this case, there are several variants, PP2 and PP3):

First of all, 2 protons fuse (whose one that is turns into a neutron by \(\beta^+\) radioactivity, the same as above) forming Deuterium (an isotope of hydrogen, constituted of a proton and a neutron). A neutrino is emitted, as well as a positron (anti-electron; anti-matter), which almost instantly annihilates in energy with an electron (given that it is in a 'cloud' of free electrons), notably in the form of gamma rays (very high energy photons). Deuterium fuses with another proton, forming helium-3, and a lot of energy is again emitted. Finally, 2 helium-3 atoms fuse to form helium-4, accompanied by 2 neutrons, again releasing a lot of energy. Let the following reaction equation:

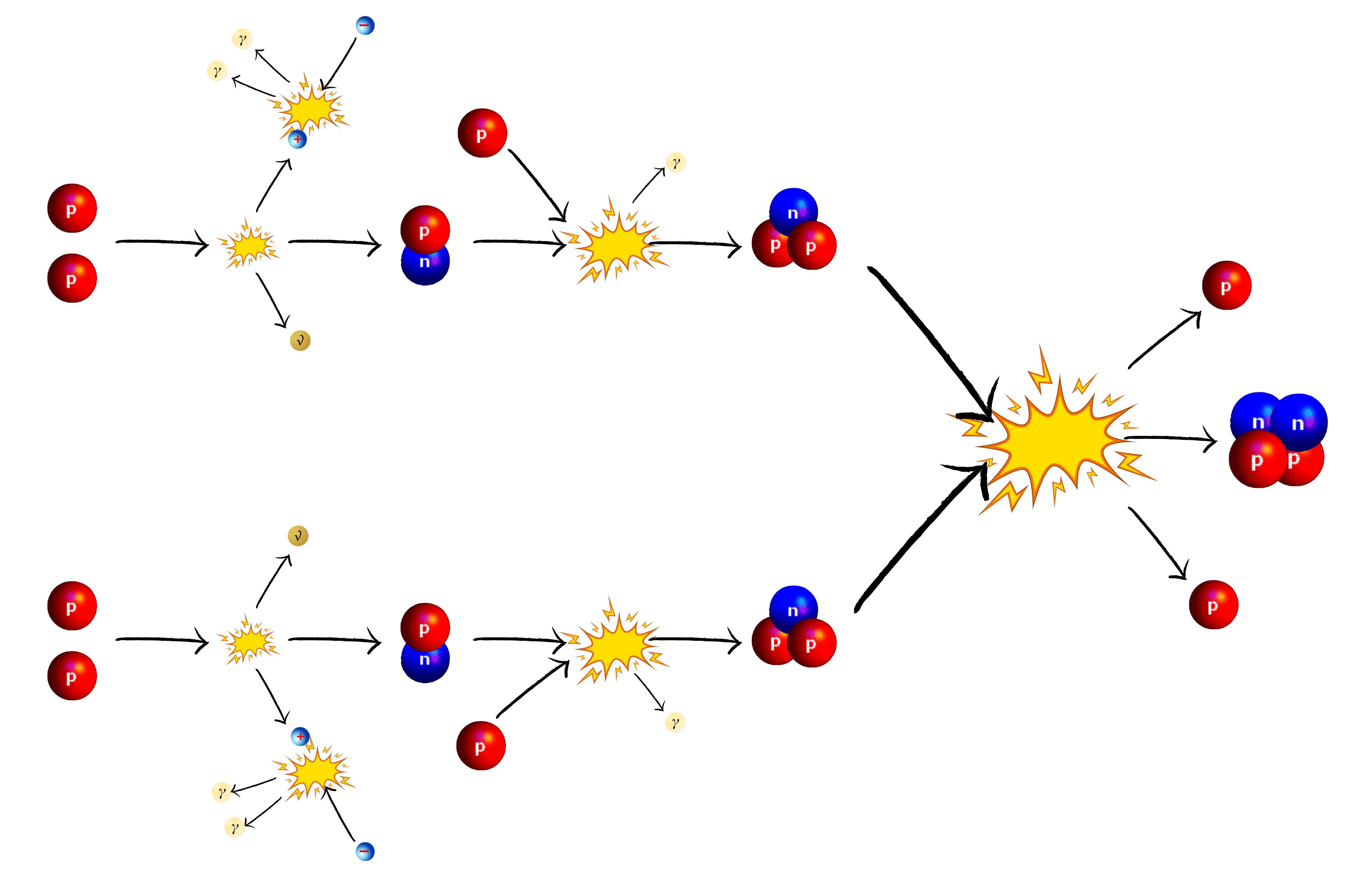© MH info Proton-proton chain diagram

As a reminder, fusion reactions are theoretically impossible, but only occur because of the quantum tunnelling (which happens about once every 100 billion collisions), and \(\beta^+\) radioactivity (1 out of 1 million billion billion collisions). In cases where radioactivity does not occur, the protons separate because of their same electromagnetic charge. Finally, fortunately that fusion in the core of the Sun is not more efficient, because otherwise it would have used up all its hydrogen in just a few million years (compared to about ten billion years for a spectral G-type star), and you would not exist, even less to read this text. To demonstrate that the fusion energy released is low and fusion reactions are rare (on a small scale, of course), one can imagine that one would be in possession of a cubic meter of Sun: it would produce only 300 W. That is enough to power three small light bulbs. So, from the top of its inconceivable 1.412 x 10¹⁸ m³ (14,120 billion billion cubic meters), or about 10 zm³ (cubic zettameter), the Sun fuses about 633 million tons of hydrogen into 628 million tons of helium every second. This represents 5 million tons of hydrogen converted into energy, or 4 x 10²⁶ joules (400 yottajoules or 400 million billion billion joules!), equivalent to 10¹¹ TWh, or as much as the world's electricity consumption (as of 2018) for about 2.5 million years! To summarize these figures, which are far beyond understanding: as the sun is a plasma, there are few molecules per m³, and therefore few nuclear reactions per m³. Given its size, the energy released is phenomenal.

There is however another chain that converts hydrogen into helium, this is called the CNO cycle (carbon-nitrogen-oxygen cycle). Logically, for that the CNO cycle occur, the star must contain carbon, which was not produced during the Big Bang (75% hydrogen and 25% helium). It was therefore impossible in primordial stars (the first stars) − with null metallicity − for the CNO cycle to occur. Moreover, the temperature required for this fusion mechanism is higher than for the proton-proton chain. Thus, the CNO cycle is the main mechanism in massive stars. In reality, carbon, nitrogen and oxygen are not really consumed during the reaction, but rather act as catalysts: they are necessary for the reaction but are reproduced at the end. We can also consider nitrogen and oxygen as intermediates products, as they are produced and then consumed during the reaction. Carbon-12 fuses with a proton to form nitrogen-13, releasing energy notably in the form of gamma rays. As nitrogen-13 is unstable, it decays by \(\beta^+\) radioactivity into carbon-13, positron and neutrino. The positron immediately annihilates with an electron, producing two gamma rays. The carbon-13 then fuses with another proton forming nitrogen-14 and a gamma ray. The nitrogen-14 fuses with a new proton, producing oxygen-15 and an additional gamma ray. Oxygen-15 is also unstable, so it also undergoes a \(\beta^+\) decay, forming nitrogen-15, a positron and a neutrino. The positron annihilates in the same way. Finally, the nitrogen-15 fuses with a proton, reproducing carbon-12 and helium-4. We find the carbon-12 that was present initially, which confirms the fact that it served as a catalyst. Let us take the following reaction equation:

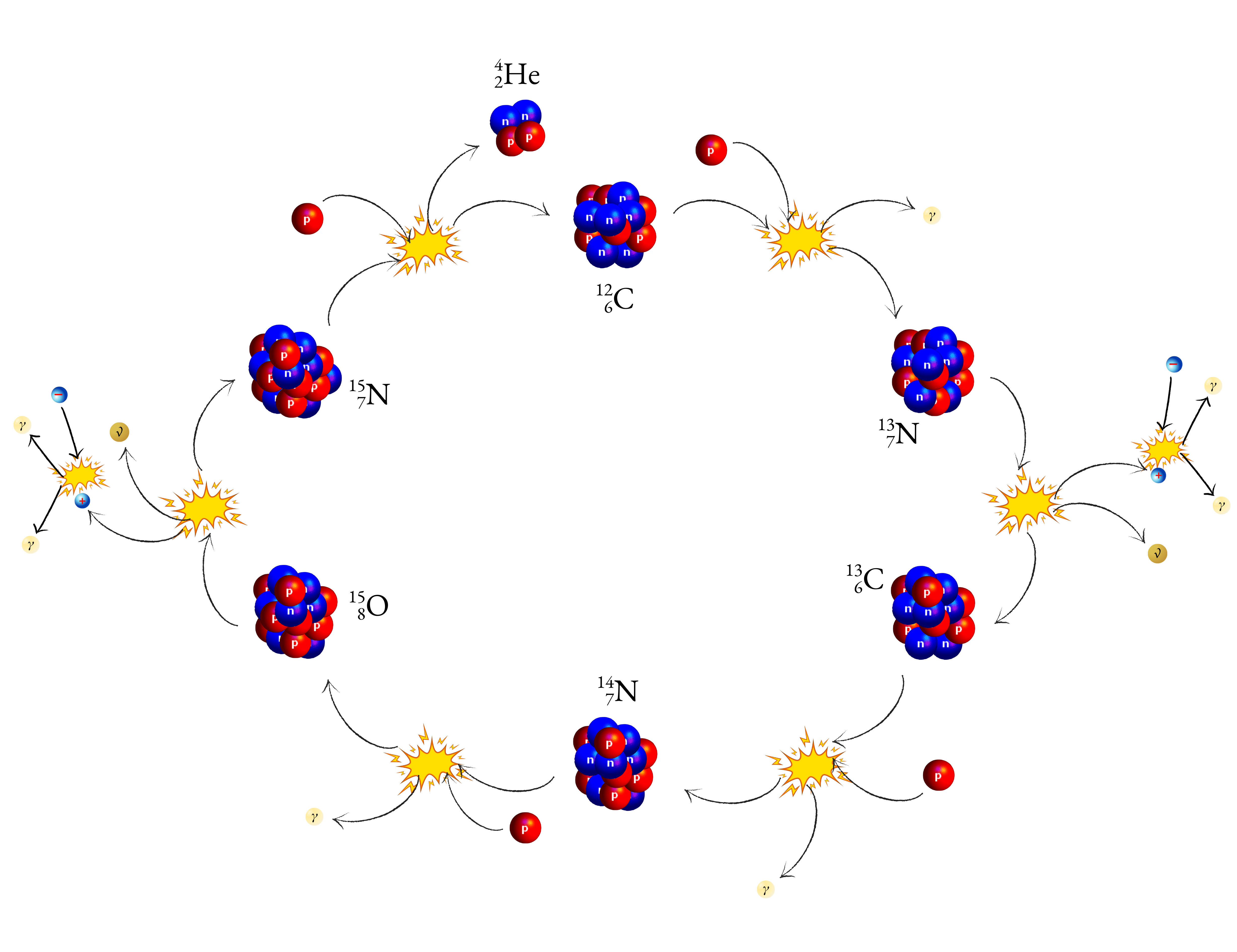© MH info CNO cycle diagram

Nuclear reactions can occur through several types of fusion in different regions of the same star: 90% of the Sun's nuclear reactions take place through the proton-proton chain, and the remaining 10% through the CNO cycle. The most substantial parameter influencing the preponderance of one type of fusion in the core of a star is temperature: the coulomb barrier (the energy barrier) required for CNO reactions is much higher than that necessary for the PP chain reactions. Therefore, the probability of the quantum tunnelling for occurring is lower for the CNO cycle than for the PP chain, which is why the PP chain is preponderant at low temperatures (and thus in lowmass stars). On the contrary, the higher the temperature, the higher the probability that the quantum tunnelling occur for the CNO cycle, and this is why the CNO cycle is predominant at higher temperatures (and thus in more massive stars). The principle is the same for the preponderance of a variant of the PP chain or the CNO cycle. The presence of more or less carbon can also come under consideration in the preponderance of the PP chain or the CNO cycle.

To illustrate these last explanations, here are some figures:

The PP chain fuses, on average, hydrogen into helium from 10⁷ K to 2.3 x 10⁷ K. The CNO cycle fuses, on average, hydrogen into helium from 1.5 x 10⁷ K, and becomes dominant in the PP chain from 1.8 x 10⁷ K.

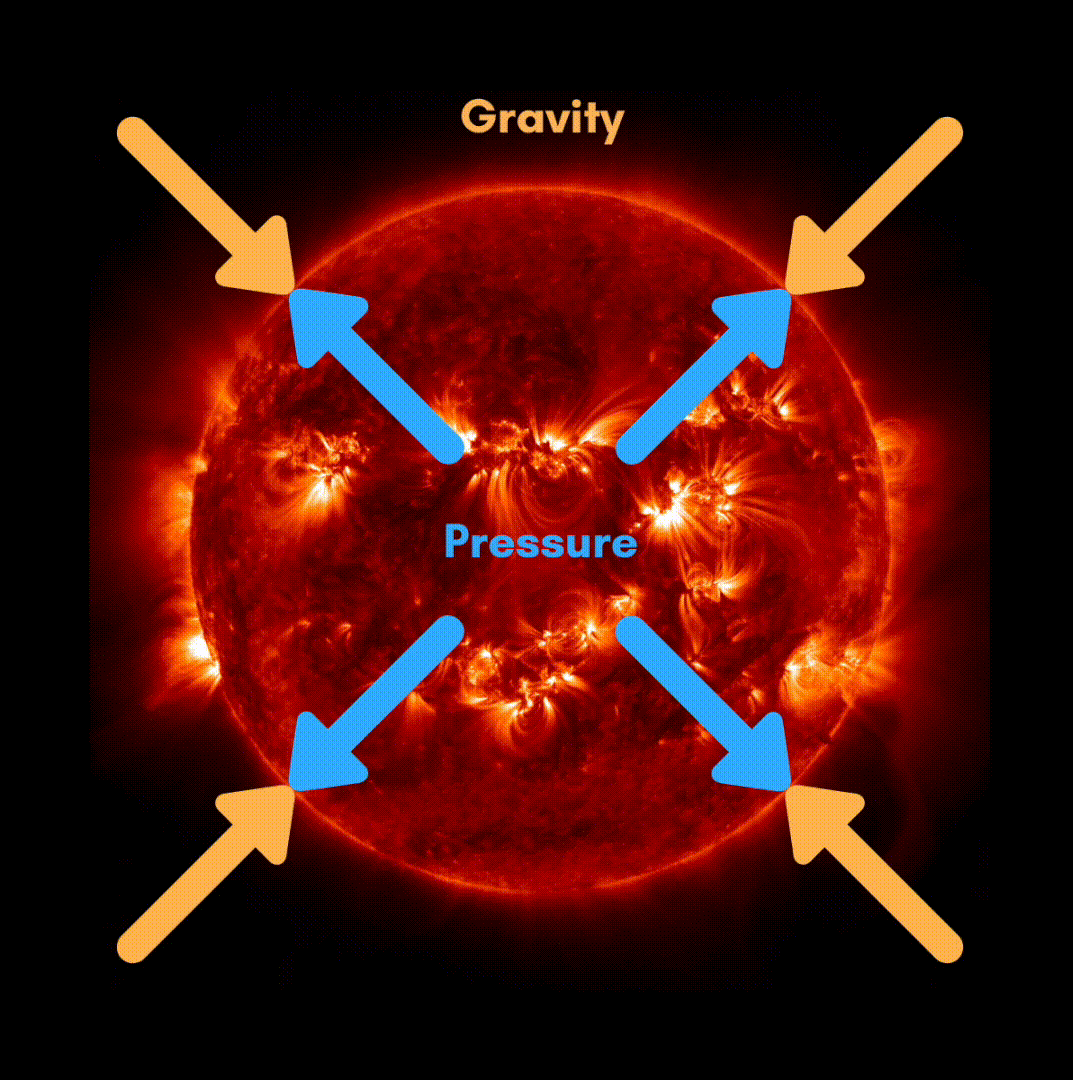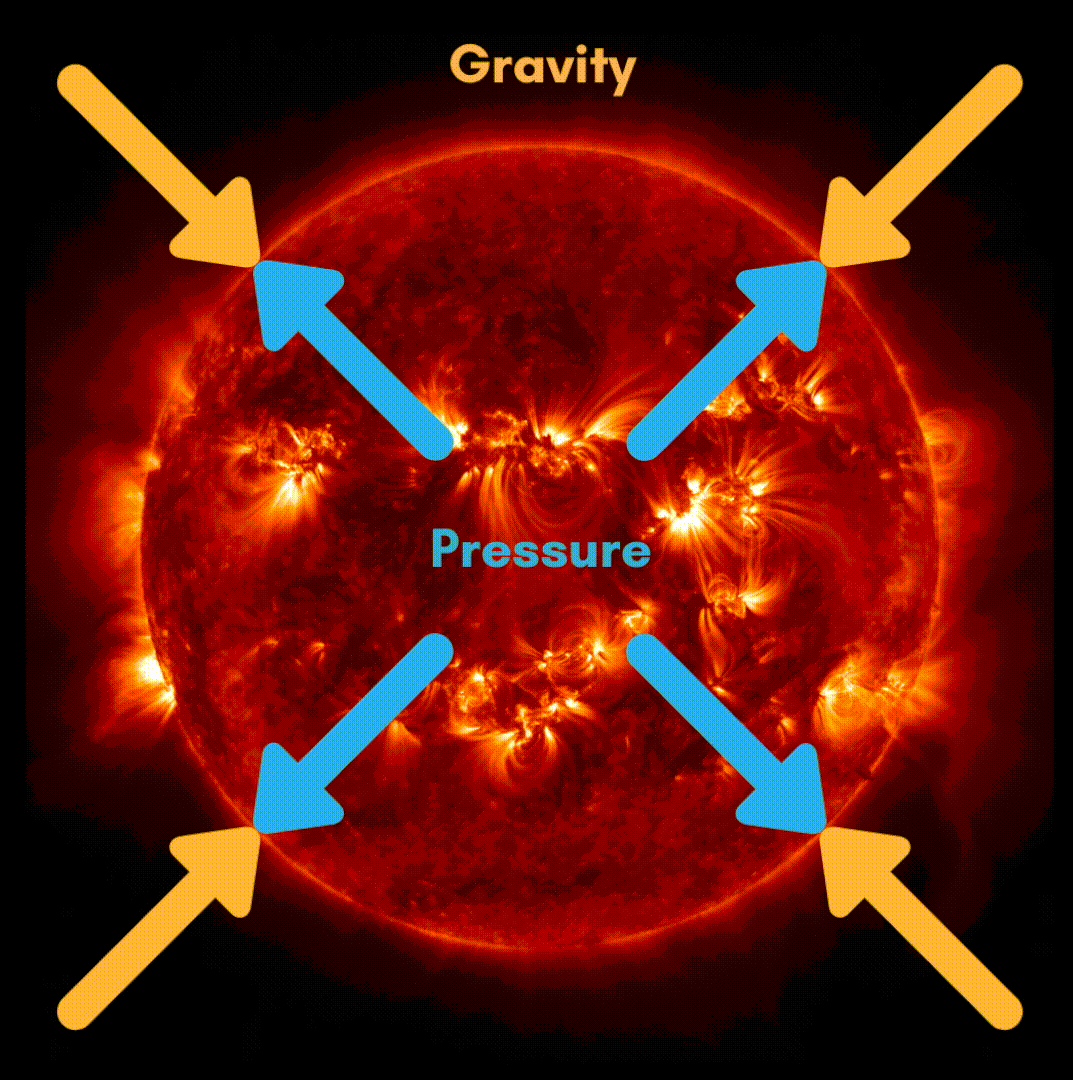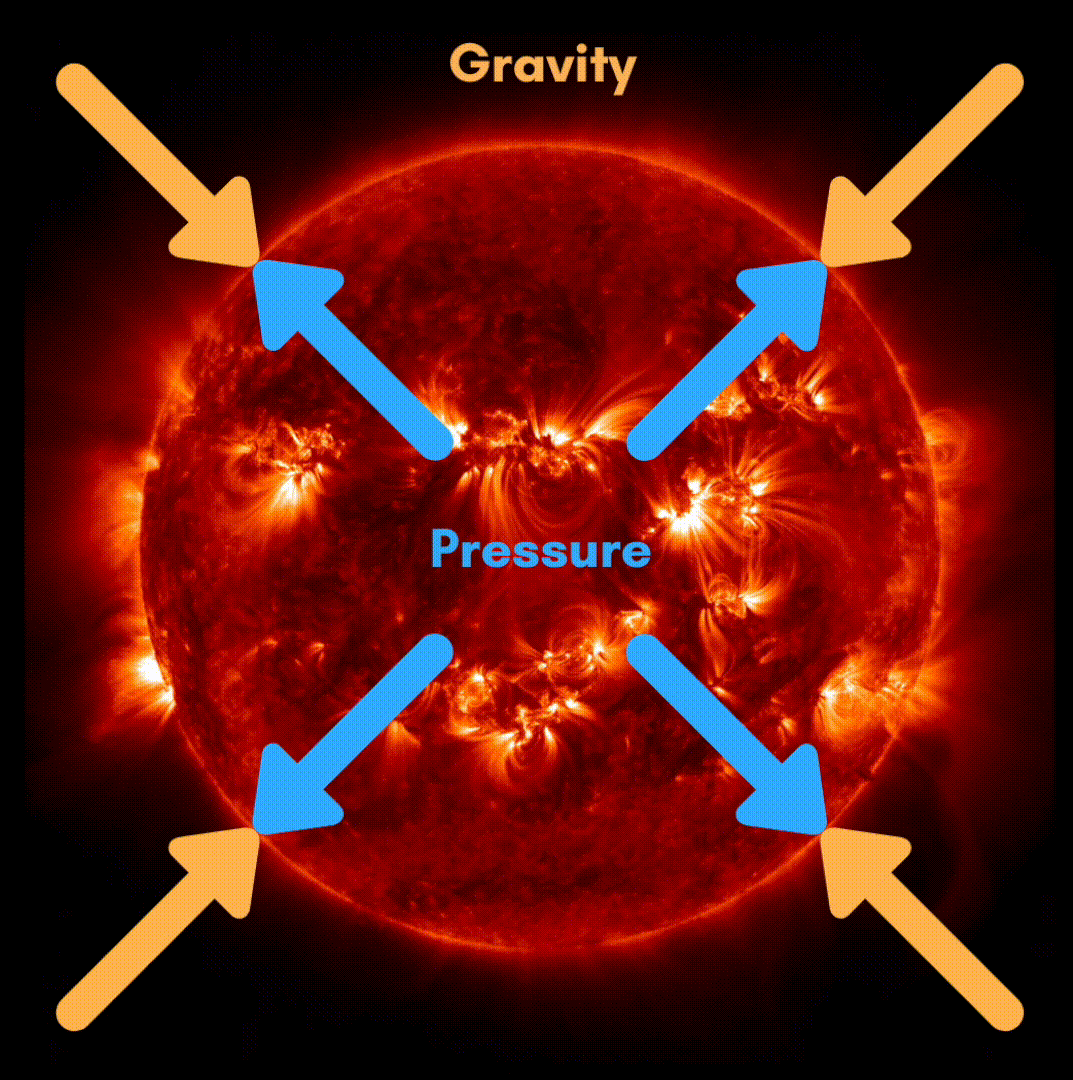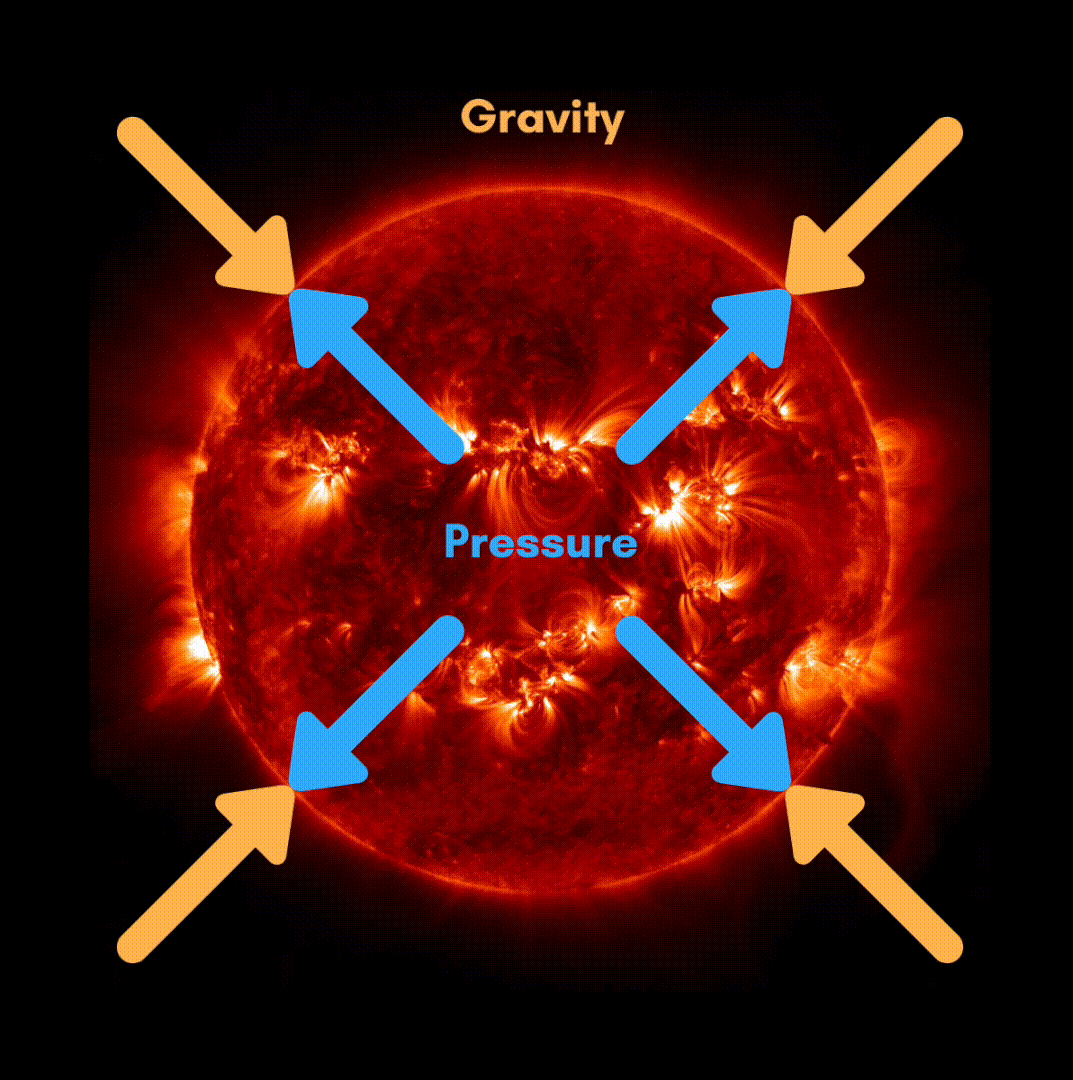
The hydrostatic equilibrium, a constant opposition

Principally two forces are opposing theme self in the stars:

• Gravity, contracting the star on itself
• The pressure in the core of the star, which causes the star to expand.

Before the nuclear reactions begin, gravity causes the star to contract on itself, raising the temperature enough to start hydrogen fusion. This generates a strong pressure, and the star expands. When these two forces stabilize, that is to say when the gravitational attraction is compensated by the action of the pressure forces, the star is said to be in hydrostatic equilibrium: when the fusion reactions decrease, the temperature drops and gravity contracts the core, which increases the temperature, restarts the nuclear reactions, heats up the core, expands it, decreasing the temperature and so on...

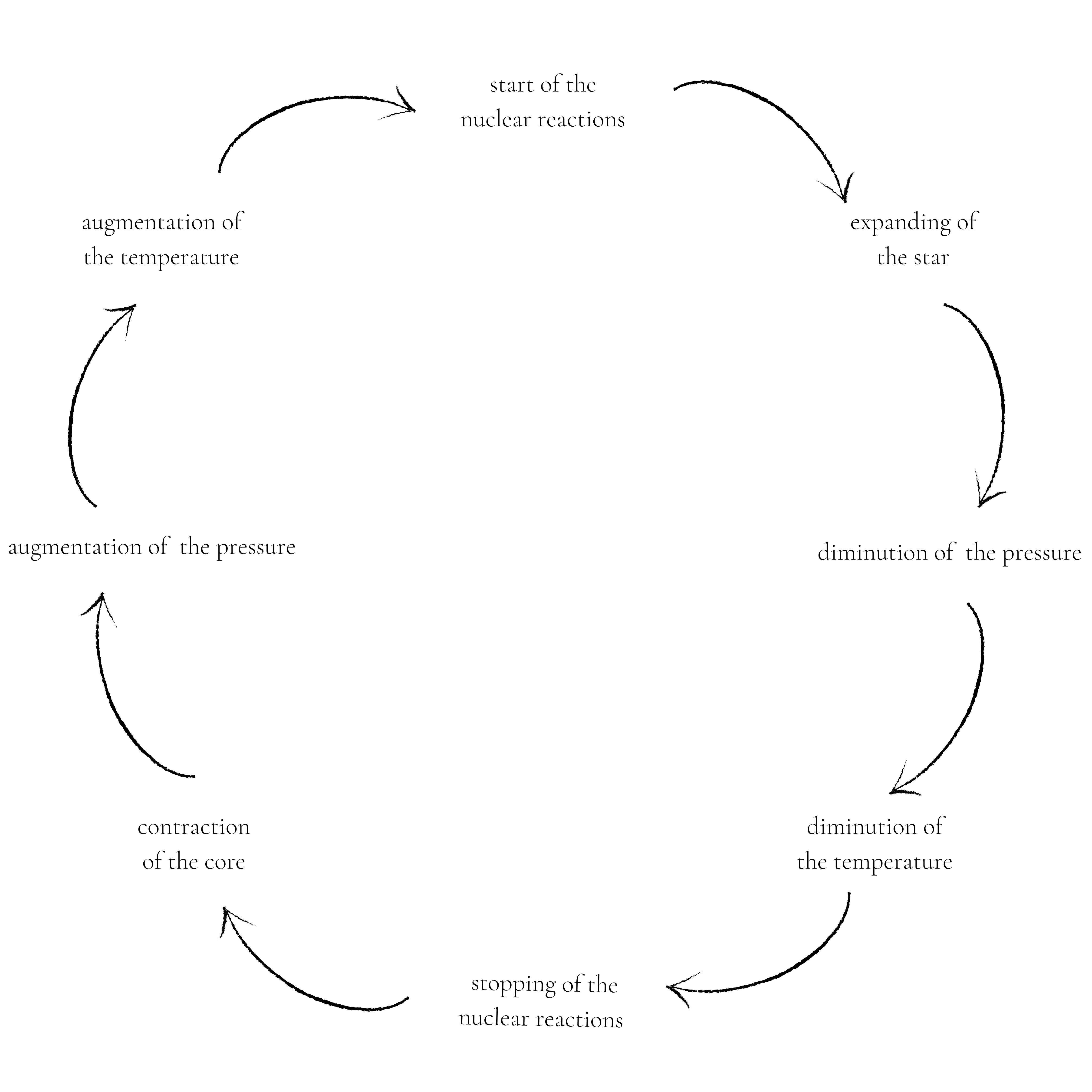© MH info Diagram of hydrostatic equilibrium

© MH info Animation on hydrostatic equilibrium

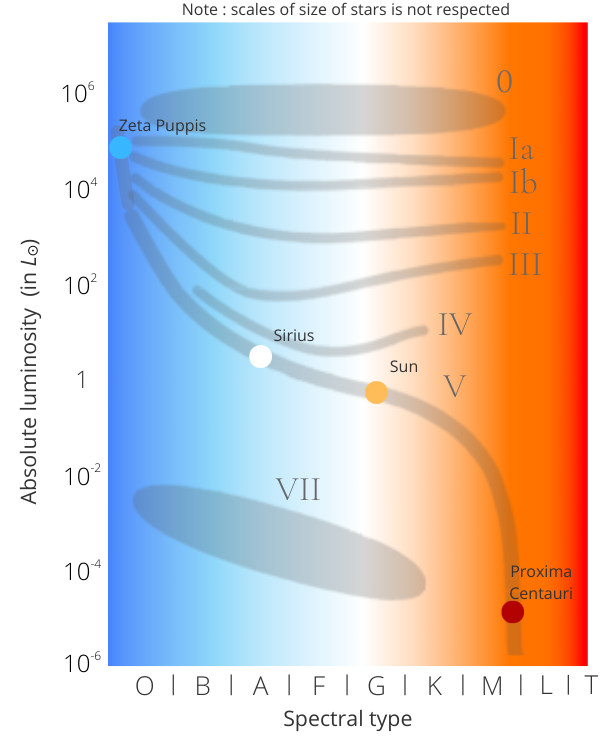
The Hertzsprung-Russel diagram, a reference tool

© MH info Hertzsprung-Russel diagram

The Hertzsprung-Russel diagram (or H-R diagram) is a graph that allows to classify stars according to their absolute luminosity (ordinate) and their spectral type (abscissa). It was developed by Ejnar Hertzsprung and Henry Norris Russel and has notably contributed to establish a theory of stellar evolution (all the phenomena from the formation to the "death" of a star). It is a reference tool in stellar astrophysics (the branch of astrophysics that studies stars), likewise the periodic table of elements in chemistry. Indeed, the word stellar means related to stars, from the latin 'stella' meaning star.

Luminosity (in astronomy) is the amount of energy emitted by any celestial body per unit of time.

We can distinguish two types of luminosity:

• Relative luminosity is the brightness we perceive from our position and is therefore dependent of the distance to the celestial body.
• Absolute luminosity is the actual amount of energy emitted by the object.

We can calculate the absolute luminosity from the relative luminosity of the star and its distance from us by applying a mathematical relationship. With the absolute luminosity (and the temperature, which is relatively easy to obtain), we can notably calculate the radius of a star, using the Stefen-Boltzman law, established between 1879 and 1884 by Joseph Stefen and Ludwig Boltzman.

We can determine the surface temperature of a star using Wien's displacement law, discovered at the dawn of the 20th century by Wilhelm Wien:

The Greek letter \(\lambda\) (lambda) is used in physics as a symbol of the wavelength: \(\mathrm{\lambda_{max}}\) thus corresponds to the most emitted light the wavelength. \(T\) corresponds to the absolute temperature (in Kelvins) and 2, 89777291 × 10⁻³ the Wien constant.

To find \(\mathrm{lambda_{max}}\), we use an electromagnetic spectrum and we search the most intense luminous flux in the spectrum.

In plain English, this formula indicates that the wavelength at which a black body emits the most luminous flux (light power) is inversely proportional to the temperature of that body. The black body is an ideal object, which would absorb all the electromagnetic radiation it receives, use it to heat itself and then emit radiation, called black body radiation. There are, however, bodies that behave in a similar way to a black body: stars, incandescent lamps, heated (incandescent) metals or lava.

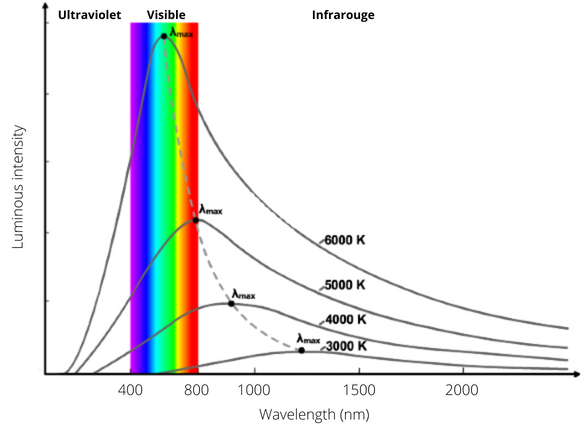© MH info © Hafhalifax magazine Spectrum of black body radiation

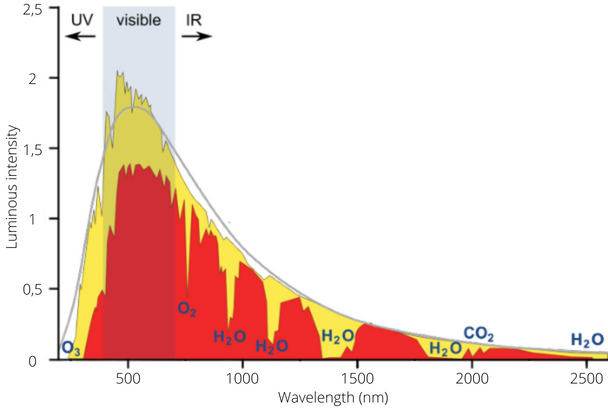© MH info © Cosmodixi Spectrum of solar radiation compared to that of a black body at 5800 K: in yellow, the real solar spectrum before the passage of its light through the Earth's atmosphere, and in red, the solar spectrum observed on the ground, after the passage of its light through the Earth's atmosphere. In blue, the absorption lines corresponding to the chemical elements present in the Earth's atmosphere.

We are looking for \(T\), so:

$$T = \frac{2,89777291\ \times \ 10^{- 3}\ }{\lambda}$$

For example, the colour that the Sun emits the most is green, that is to say a wavelength of about 500 nm. Its surface temperature is therefore about 5800 K:

$$T = \frac{2,89777291\ \times \ 10^{- 3}\ }{0,0000005} \approx 5800\ K\ \mathrm{(being\ 6100{^\circ}C)}$$

For a body whose most emitted light corresponds to a wavelength of about 600 nm (red), its surface temperature is about 4830 K:

$$T = \frac{2,89777291\ \times \ 10^{- 3}\ }{0,0000006} \approx 4830\ K\ \mathrm{(being\ 5130{^\circ}C)}$$

We can therefore deduce that the shorter the wavelength, the higher the temperature. The reason is simply because the hotter a body is, the more energy the photons emitted have. But the more energy a photon has, the shorter its wavelength (and the higher its frequency, for information).

An indispensable source of information: the light

Stellar spectroscopy (or spectrometry) is the study of the electromagnetic spectrum of stars, that is to say the study of the decomposition and of the classification of electromagnetic radiation from stars.

The absorption and emission lines of the observed spectrum allow the composition of stars to be determined. Here is a short digression allowing to understand what absorption and emission lines are:

Electrons can move up one energy level (associated to an orbital) by absorbing energy or down one level by emitting energy − usually a photon. Therefore, the further an electron is from the nucleus of the atom to which it belongs, the higher is his energy. When an electron absorbs a photon, it is said to be excited. The photon that the electron must absorb or emit to change energy level has a very specific wavelength, corresponding to the energy needed to change from one level to another. Given that only certain extremely precise levels are allowed (see the "Did you know?" on the electronic degeneracy ; it is not available in English) and since they depend on the atom, they are calculable − and calculated. These calculations have been the subject of decades of experimentation, in order to know the precise amount of energy (or wavelength) required for an electron to move from one level to another, whatever of the level or the atom. Imagine that we send a beam of white light into a environment containing a certain element and then decompose this beam: the corresponding lines at a wavelength of 656 nm, 486 nm, 434 nm, 410 nm and 396 nm are no longer present (this is represented by a black line on an electromagnetic spectrum). This means that the light beam has passed through a environment containing hydrogen! We can therefore take the electromagnetic spectrum of the light coming from the surface of a star and deduce its composition.

© Schoolmouv Hydrogen absorpotion spectrum

Conversely, when an electron is in an excited state, there comes a time when it must de-excite, by releasing energy: the hydrogen atom's electron emits a photon − in a random direction − corresponding to one of the above wavelengths (an element only absorbs the radiation that is able to emit). In the same way, it can be found that it is a hydrogen atom that has emitted a photon.

© Schoolmouv Hydrogen emission spectrum

According to what criteria do we classifies stars?

Romain Angelo Secchi was the first to propose a method for classifying the stars, in 1866. To do this, he based in particular on the characteristics of the electromagnetic spectra of the stars, and divided them into five classes (simply from I to V). But these classes were considered as too vague and gathers too many different stars together.

We use nowadays the Harvard classification, developed in part at the Harvard University Observatory by Henry Draper, shortly after Secchi. Unfortunately, the latter died in 1882 at the age of 45 before completing it. His wife bequeathed a lot of money to the observatory so that the classification work started by her husband could be completed. This was done notably by Williamina Fleming, who classified the stars by the intensity of their hydrogen lines, and then revised and completed by Annie Jump Cannon, who simplified and reorganised the order of the classes by temperature, from the hottest to the coldest. Finally, this classification was published in the 'Henry Draper Catalogue' (in homage to him), which included more than 225 000 stars (named 'HD', followed by a number), in the 1920s. This classification also categorises stars according to their spectrum, organised into spectral types, and consequently by surface temperature (Wien's law): according to on the temperature, the intensity of the lines changes (a hot star will have more lines with a low wavelength than a star of medium temperature). In summary, we can deduce the composition of a body using spectroscopy (and deduce from the composition of a star its age: if it has a lot of hydrogen, we can deduce that it is a young star), the relative speed of movement of the star using the Doppler effect, and the surface temperature using Wien's law, or the speed of rotation using the variation of the magnetic field. We sort the stars using the types O, B, A, F, G, K, M, L, T and Y, specifying the subclass between 0 and 9 (O0 being the hottest spectral type). An O-type star will have intense blue lines, while an M-type star will have almost no blue lines. The L, T and Y types − the brown dwarfs − added later, as well as the WR (Wolf-Rayet) and LBV types (luminous blue variable (star)). LBV stars are extremely rare, unstable, and massive. They are blue (spectral type O or B) and are located in the hypergiant luminosity class (extremely luminous): they are so much as they tend to reach the Eddington limit, established in 1921 by Arthur Eddington and observed by Edwin Hubble in the Andromeda galaxy. When this limit is reached, the pressure exerted by the star through nuclear reactions is so high that the star is no longer in hydrostatic equilibrium, and pressure takes on gravity: this causes a very intense stellar wind (a flow of gas expelled from a star) of outer layers of the star (the outer layers are literally "blown away"). It then becomes a 'simple' WR star. This limit thus corresponds to the maximum luminosity that a star can reach, defined in terms of its mass.

Furthermore, the spectral type defines the star in question at a given moment (its type evolves over time, see comparison below)

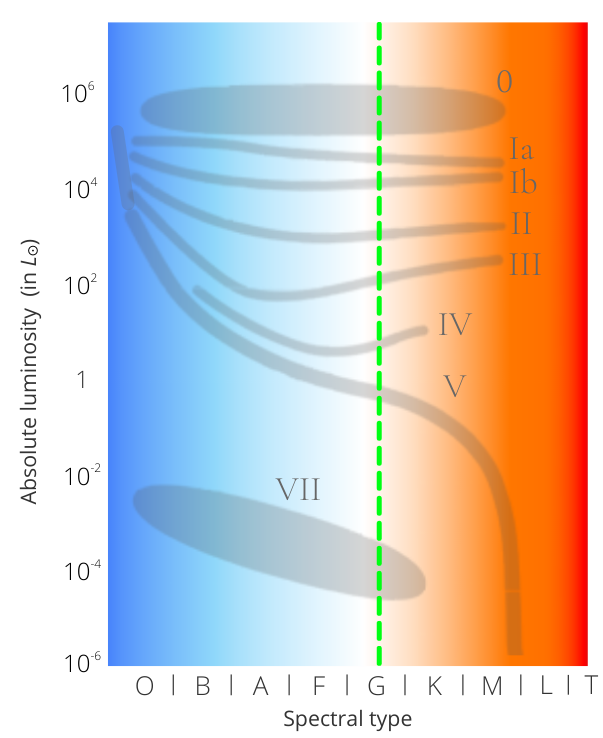
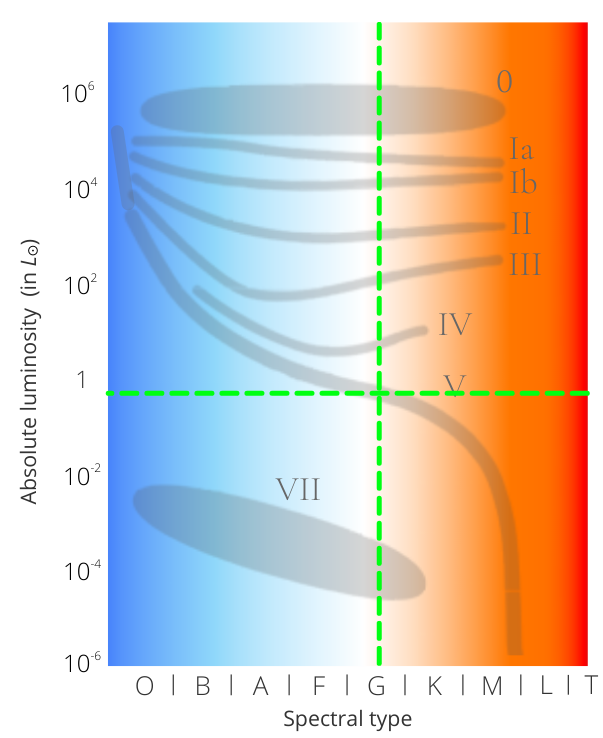
Stars are also classified by absolute luminosity, according to the MKK classification (William Morgan - Philip C. Keenan - Edith Kellman) developed later, in 1943. It is presented in 8 luminosity classes (or branches) ranging from 0 to VII:

• Hypergiants (0): This class was added after the discovery of even brighter stars
• Supergiants (Ia and Ib)
• Bright giants (II): Intermediate class, more luminous than the giants, but less than the supergiants.
• The giants (III)
• Subgiants (IV): Intermediate class, more luminous than the main sequence stars, but less luminous than the giants.
• Main sequence (V): This represents the overwhelming majority of stars, as it is the longest period of their life, in compliance with what was seen at the beginning of the article.
• Sub-dwarfs (VI): A little used term.
• White dwarfs (VII): A white dwarf is the dead body of a star, usually at the centre of a planetary nebula. It is very dense: 1 teaspoon would weigh nearly a ton.
  The classification of stars is done according to their spectrum and absolute luminosity. To classify a star, we add the number corresponding to the luminosity class, after the spectral type and the subclass (F3 V for example). This allows to place the star in time, at contrary to the spectral type alone: a G-type star can theoretically be in the main sequence as well as in the giant branch, or evolve into an M-type star... By adding the luminosity class, we can place the star precisely in the diagram, whereas with the spectral type alone, we can only place it on one line (it can theoretically be on almost any branch). Here is a diagram that will surely be clearer:

© MH info Classification table of main sequence stars

Final phase of stellar evolution: a hectic period in the life cycle of a star

From the very instant a star starts to shine, it fuses the hydrogen located in its core into helium. Logically, the more hydrogen it consumes, the less hydrogen is available, so there comes a time when there is none left. When hydrogen resources are exhausted, hydrogen fusion stops, just as when there is no more combustible in a fire, combustion stops.

There is, however, one problem: remember hydrostatic equilibrium! Their further evolution will be determined by their masses:

Stars of less than 0.08 M_☉ (brown dwarfs):

These stars cool forever without really having a main sequence: it is a 'stillborn' star, which will gradually become a white dwarf, then a black dwarf, the hypothetical evolution of a white dwarf, which has cooled so much that it no longer shining. It approaches the temperature of absolute zero (0 K or -273.15 °C/-459.67 °F) and is hypothetical because the Universe is still (much) too young to have the possibility of detecting such a cooled white dwarf. Even if the Universe were old enough, it would be difficult to detect them (they emit radiation just above microwaves, which is difficult to detect).

Stars included between 0.08 and 0.3 M_☉ (red dwarfs):

After an extraordinarily long stay on their main sequence, they cool down, evolving into white dwarfs and then black dwarfs.

Stars included between 0.3 and 8 M_☉ (most spectral types):

These ones contract on herself and the temperature rise again: enough for the hydrogen around the core to start fusing, and they gradually expand to start their next phase as a red giant: they move up the diagram and shift to the right (their luminosity increases and their temperature decreases). Once the hydrogen in the outer layers is depleted, the star finally contracts on herself again, and begins to heat up. Stars with a mass between 0.3 and 2 M_☉ become so dense that the helium in their core becomes degenerate (see the "Did you know?" on the electronic degeneracy ; it is not available in English): the temperature is not high enough to start the fusion of helium  − which would generate a thermal pressure that would restore hydrostatic equilibrium − and the core continues to collapse on itself. When the temperature reaches 100,000,000 K, the helium begins to fuse through the triple alpha chain (or triple-𝛼), fusing 3 alpha particles (helium-4 without electron − nucleus of helium atom) into carbon-12, via beryllium. Let the following reaction equation:

$$\mathrm{_{2}^{4}{He}} + \mathrm{_{2}^{4}{He} \rightarrow_{4}^{8}{Be}}\ + \gamma$$

$$\mathrm{_{4}^{8}{Be}} + \mathrm{_{2}^{4}{He} \rightarrow_{6}^{12}C}\ + \gamma$$

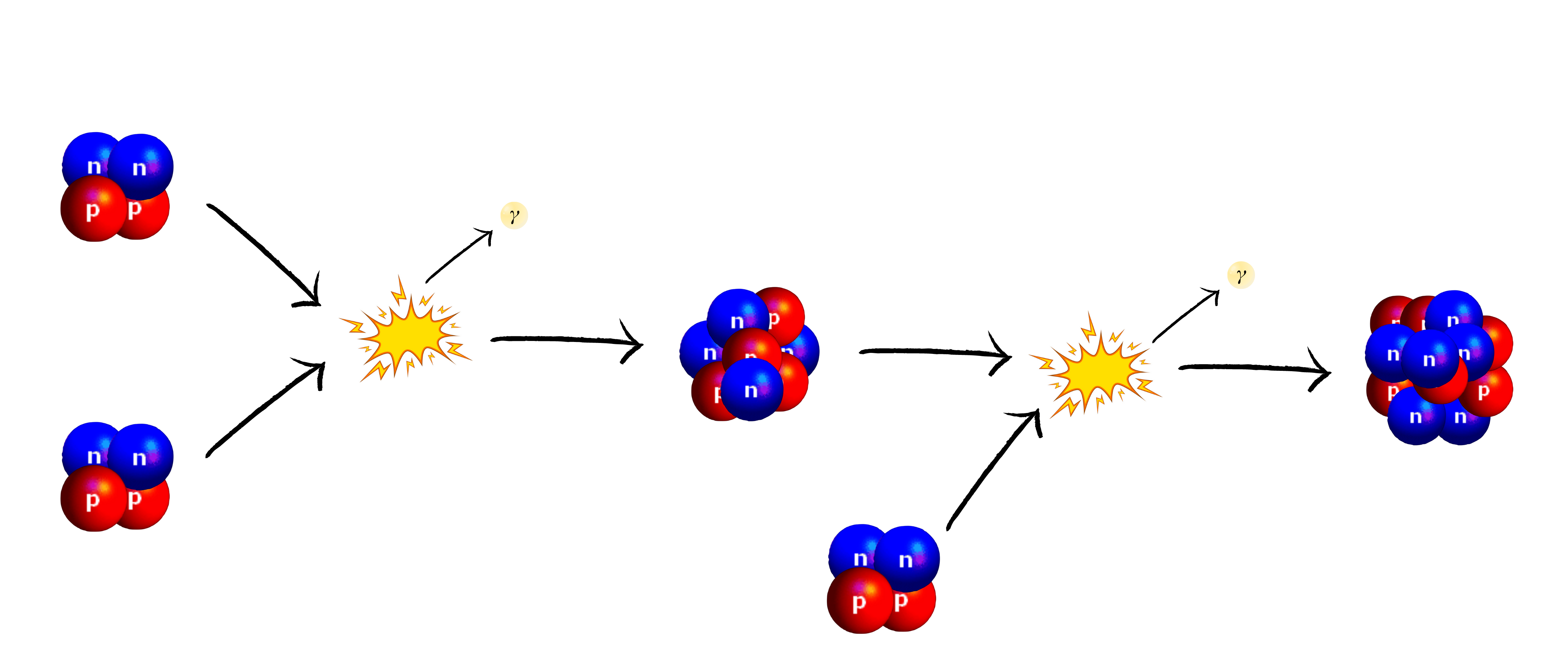© MH info Diagram of the triple alpha chain

The star is now located in the branch called "horizontal branch".

The temperature increases, but not the pressure: as helium is degenerate, the pressure depends mostly on the density. The rate of fusion increases because of the temperature, producing even more heat... There is therefore no pressure, which normally regulates nuclear reactions: the fusion of helium goes into overdrive. A shock wave is produced, and the pressure finally becomes brutally thermal. The degeneracy is lifted, and the law of perfect gases applies again: the star suddenly expands. This phenomenon is called the 'helium flash' because it lasts only a few seconds and releases a lot of energy, but is not directly observable from the surface of the star (by electromagnetic radiation) because it produces in the core of the star.

Stars with a mass between 2 and 8 M_☉ reach the temperature required for helium fusion (10⁸ K) before the helium becomes degenerate.

The star will remain a red giant as long as there is helium left to fuse, now located in the know as 'the asymptomatic branch of giants'. Some of the carbon produced can fuse with helium to finally produce oxygen-16. Let the following reaction equation:

$$\mathrm{_{6}^{12}{C}} +\mathrm{_{2}^{4}{He} \rightarrow_{8}^{16}O}\ + \gamma$$

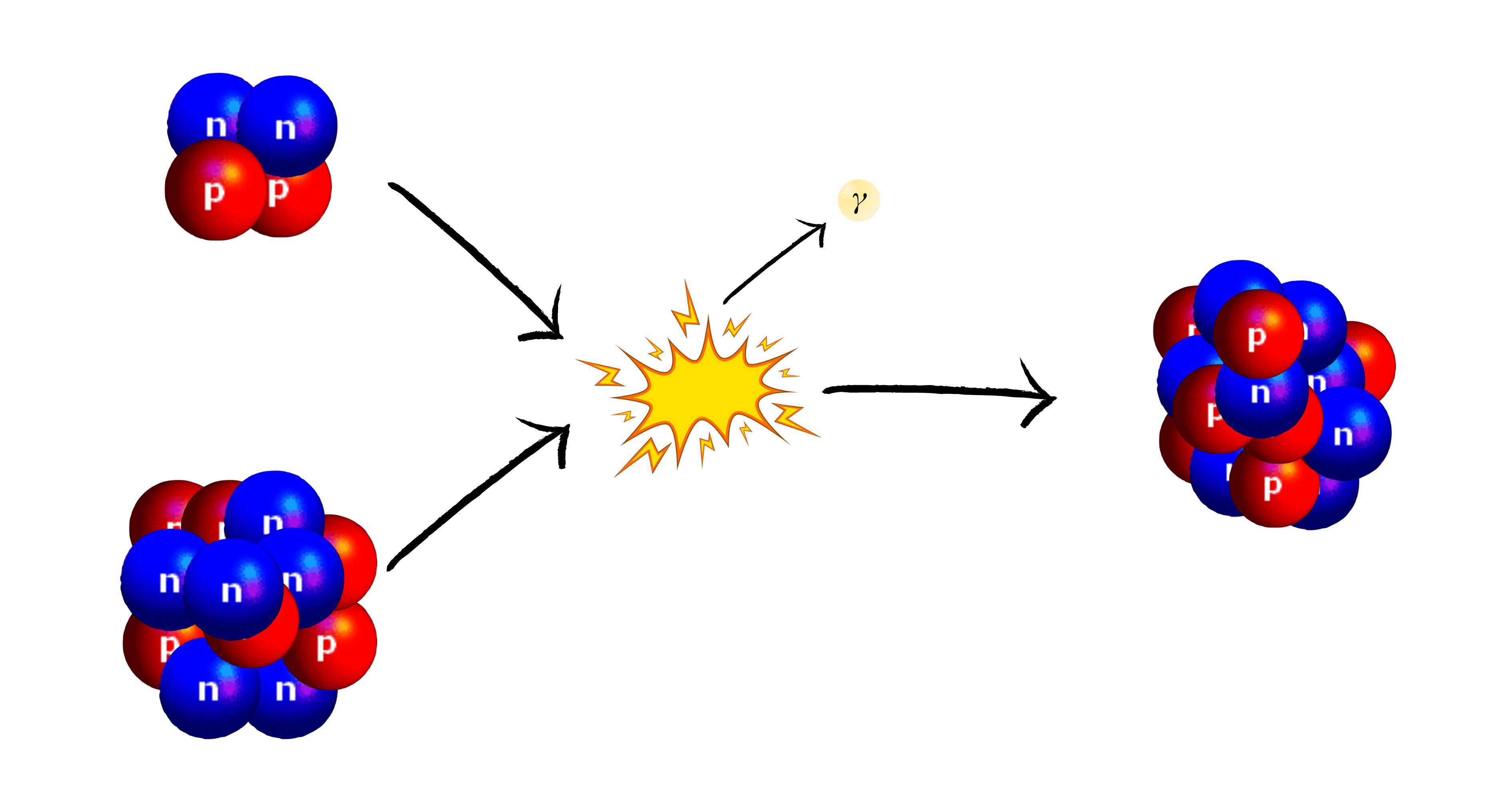© MH info Diagram of the fusion of carbon and helium into oxygen

Gradually, hydrogen and helium fusion move outwards (the star heats up as a whole, and regions further and further away from the core reach the temperatures required for hydrogen and helium fusion, 3 x 10⁷ K (CNO cycle) and 10⁸ K (triple-α chain) respectively), leaving a core of mainly carbon-12 and oxygen-16. Hydrogen fusion stops, arriving in a region of the star that is too cold. On the other hand, helium fusion continues to move outwards, heating up the star: hydrogen fusion resumes, then stops again when it reaches a region that is too cold, and so on... These are called 'thermal pulses', causing instabilities and stellar winds. The meeting of two stellar winds produces a shock wave (helium fusion progresses faster than hydrogen fusion): the star ejects its outer gas layers (mainly helium and hydrogen) to form a planetary nebula. At the centre of the nebula will be the corpse of a star: a white dwarf, made up largely of carbon and oxygen, which will remain there forever to cool down and become a black dwarf. A white dwarf is so dense that a teaspoon would weigh nearly a ton. Above 1.44 M_☉ − the mass of Chandrasekhar − the white dwarf evolves to supernova.

A planetary nebula is a large cloud of gas, generally of circular or oval shape, which emanates from the expulsion of the gas layers of a star. A white dwarf is usually found at its centre. The adjective 'planetary' is only historical: it comes from the fact that, when they are observed at a low resolution (they were discovered in the second half of the 18th century), they look like planets. The term was retained, but they have indeed no connection with planets.

Finally, if the white dwarf and the nebula are no longer in nuclear fusion, could we not observe them? Indeed, white dwarfs emit thermal radiation (in the ultraviolet range), which allows the nebula to be ionised and the beauty of these stars to be observed. Thermal radiation is generated by the thermal agitation of the atoms, thus cooling the matter. So much so that their lifespan is limited to about ten thousand years, when the white dwarf has cooled sufficiently to no longer emit UV radiation and the nebula is too diluted in space: it has an average expansion speed of 10 km/s!

Stars included between 8 and 20 M_☉ (massive stars):

These stars begin their evolution in the same way as stars with masses between 0.3 and 8 M_☉. They contract and the temperature rises again: enough that for the hydrogen around the core begin to fuse, and they gradually expand to begin their path to their next red giant phase: they move up the diagram and shift to the right. Once the hydrogen in the outer layers is used up, the star finally contracts again, and starts to heat up again.

These stars, more massive, therefore reach a temperature of 10⁸ K before the helium core degenerates: the helium flash will not produce. This fusion will take place more calmly, without a runaway reaction. Likewise after hydrogen fusion, the helium fusion reactions stop (since the internal helium has been fused). Again, the core contracts. In the same way as the helium flash for stars with masses between 0.3 and 2 M_☉, carbon fusion will be explosive, to say the least. This phenomenon will be called carbon detonation:

The contraction makes the core of these stars so dense that the carbon in their centre becomes degenerate. When the temperature reaches 600,000,000 K, carbon fusion can begin, by the fusion of two carbon-12 atoms:

• into mainly neon-20, let the following reaction equation:

$$\mathrm{_{6}^{12}{C}} + \mathrm{_{6}^{12}{C} \rightarrow_{10}^{20}{Ne}\ +_{2}^{4}{He} + 4,617\ MeV}$$

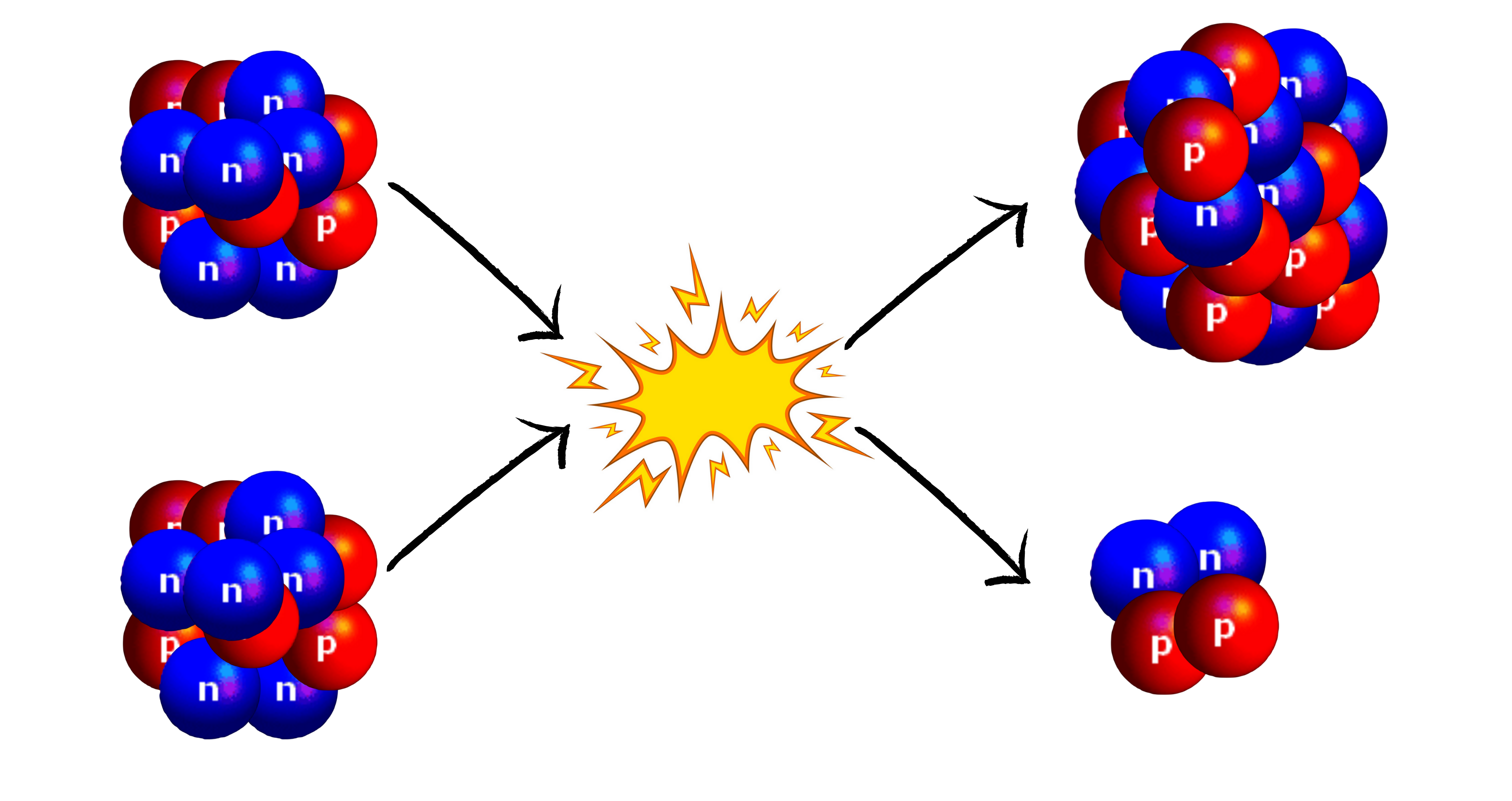© MH info Diagram of the fusion of carbon-12 to neon-20

• But also in sodium-23, let the following reaction equation:

$$\mathrm{_{6}^{12}{C}} + \mathrm{_{6}^{12}{C} \rightarrow_{11}^{23}{Na}\ + 2,241\ MeV}$$

• Or magnesium-23, let the following reaction equation:

$$\mathrm{_{6}^{12}{C}} + \mathrm{_{6}^{12}C + 2,599\ MeV \rightarrow_{12}^{23}{Mg}\ + n}$$

As the carbon is degenerated, the temperature increases, but not the pressure. The rate of fusion increases because of the temperature, producing even more heat... The fusion of carbon goes into overdrive. The stellar winds produced by this phenomenal energy move much faster this time than for less massive stars: they exceed the speed of sound (which is not 340 m/s, it changes according to the environment), thus creating a shock wave (see "Did you know? What is a supersonic bang?" coming soon). The outer layers of the star are then literally blown away in an extraordinary and impressive explosion: a supernova. Some of the electrons in the compressed residue at the centre of the remnant (matter ejected during a supernova explosion) are forced to enter the atomic nuclei by fusing with protons, which consequently become neutrons, producing an extraordinary quantity of neutrinos. This process is called URCA, which is supposed to participate in the cooling of neutron stars and white dwarfs. The amount of neutrons also increases considerably (\( p^+ + e^- + \rightarrow n + \nu_e \)). This residue is simply called a neutron star.

The properties and composition of these stars with a density close to that of a black hole are not well known: they contain on average between 1.5 and 3 M_☉ in a sphere of about 20 km.

Their speed of rotation is very high (can reach up to 716 revolutions per second): due to their contraction and by conservation of angular momentum, their speed of rotation increases considerably. For example, the momentum of a force with compared to a point is a physical quantity that expresses the capacity of this force to make a point rotate around this point. On the other hand, the linear momentum is a physical vector measure (measure represented and defined by one or more vectors), which is conserved in an isolated system (that is to say without interaction with its environment), and is defined by the product of the mass and the speed of the object. Let: \( p = mv \). The angular momentum is said to be the momentum of the linear momentum: that is to say, it is the product of the linear momentum and the radius (the momentum of a vector (in physics, thus) is always defined by a radius). The angular momentum is a vectorial measure which is, in an isolated system (a star get close, as the influence of other bodies (planets, other stars...) negligible (as it is for the black body) - except in the case of a double star), a constant which is \( L = R \cdot m \cdot V \) for a mass \( m \) (in kg) rotating at a distance \( R \) from the axis (in meters), with a linear speed \( V \) (in m/s). For reasons of practicality, we use the angular speed, represented by \( \omega \) (\( V = R \cdot \omega \)). This gives: \( L = m \cdot R^2 \cdot \omega \) for a mass \( m \) (in kg) rotating at a distance \( R \) from the axis (in m), with an angular velocity \( \omega \) (in rad/s). To use the unit tr/s and not rad/s (more convenient), we must add \( 2\pi \) (\( 1\mathrm{rad} \cdot 2 \cdot \pi \)), that is to say \( L = 2\pi \cdot m \cdot R^2 \cdot \omega \). For example, if we take a mass \( m = 1 \) rotating at a distance \( R = 3 \) from the axis at an angular velocity of \( \omega = 1 \) : \( L = 2\pi \cdot 1 \cdot 3^2 \cdot 1 \simeq 56 \ \mathrm{kg} \cdot m^2 \cdot s^{-1} \). If \( R \) is divided 3 (\( R = 1 \)), only \( \omega \) can change (\( m \) cannot change in an isolated system and \( L \) is a constant) : \( 56 = 2\pi \cdot 1 \cdot 3^2 \cdot \omega \). It is now sufficient to solve the equation, so \( \omega \simeq 9 \). Note that \( R \) has been divided by 3 and that \( \omega \) has been multiplied by \( 3^2 \): we can deduce that the angular speed varies as the inverse of the square of the radius!

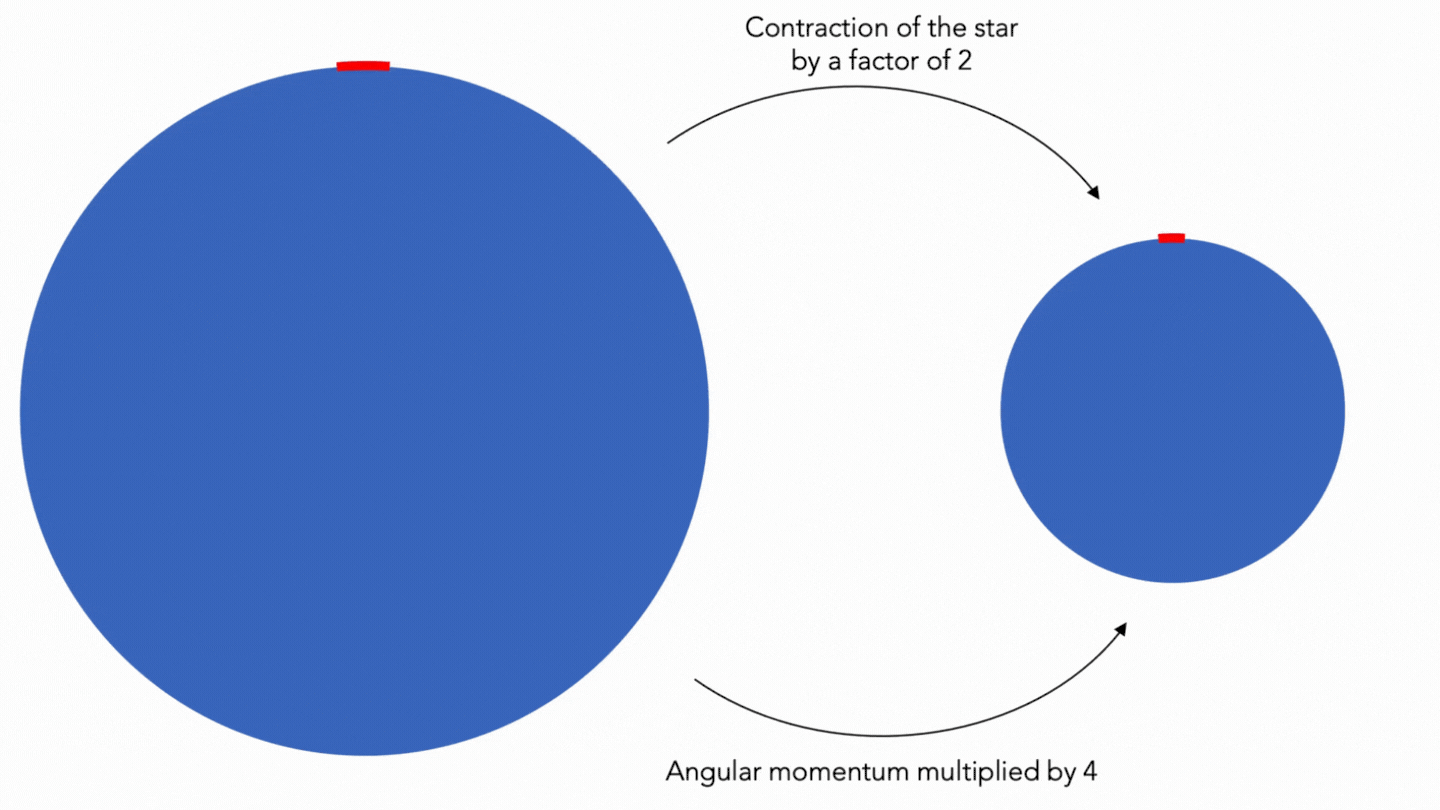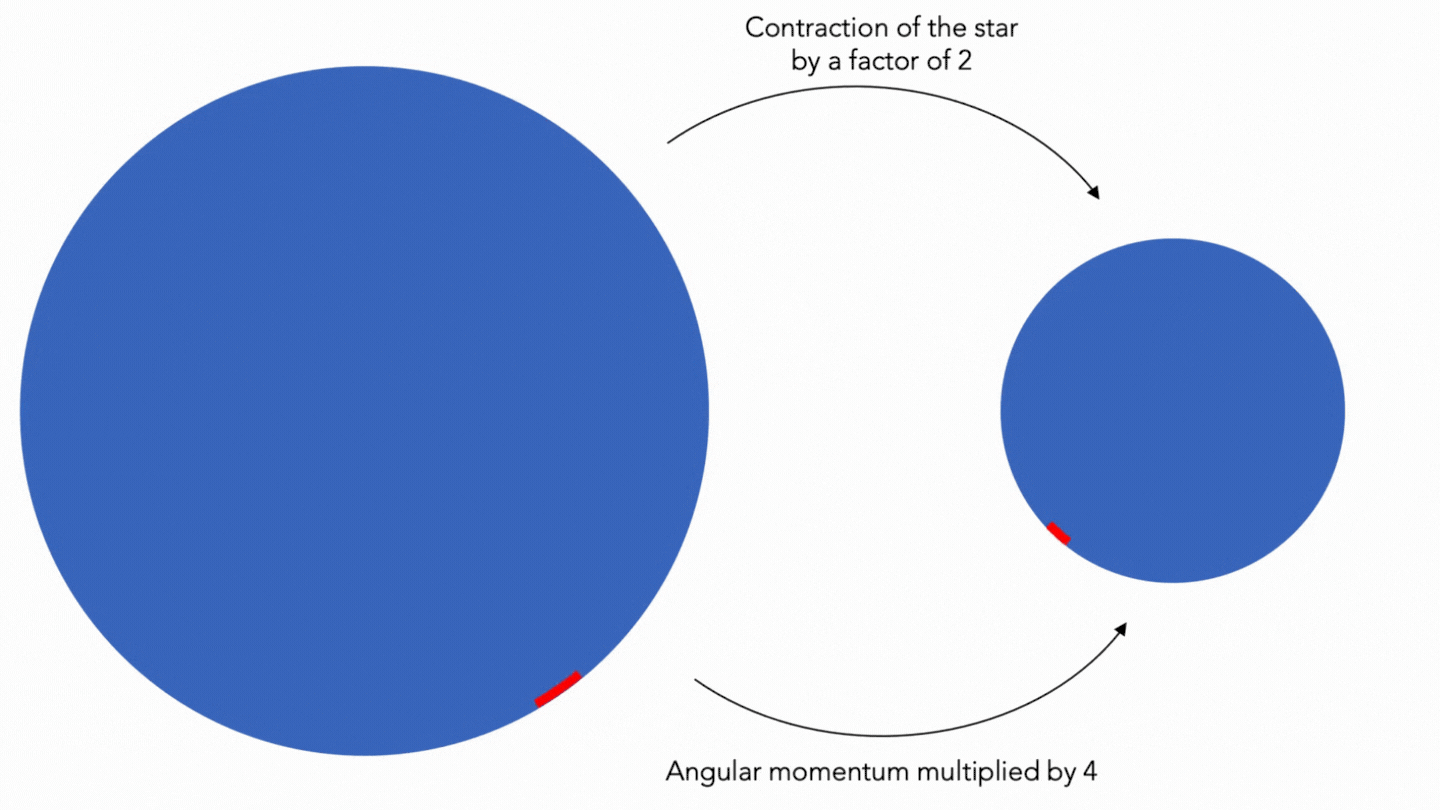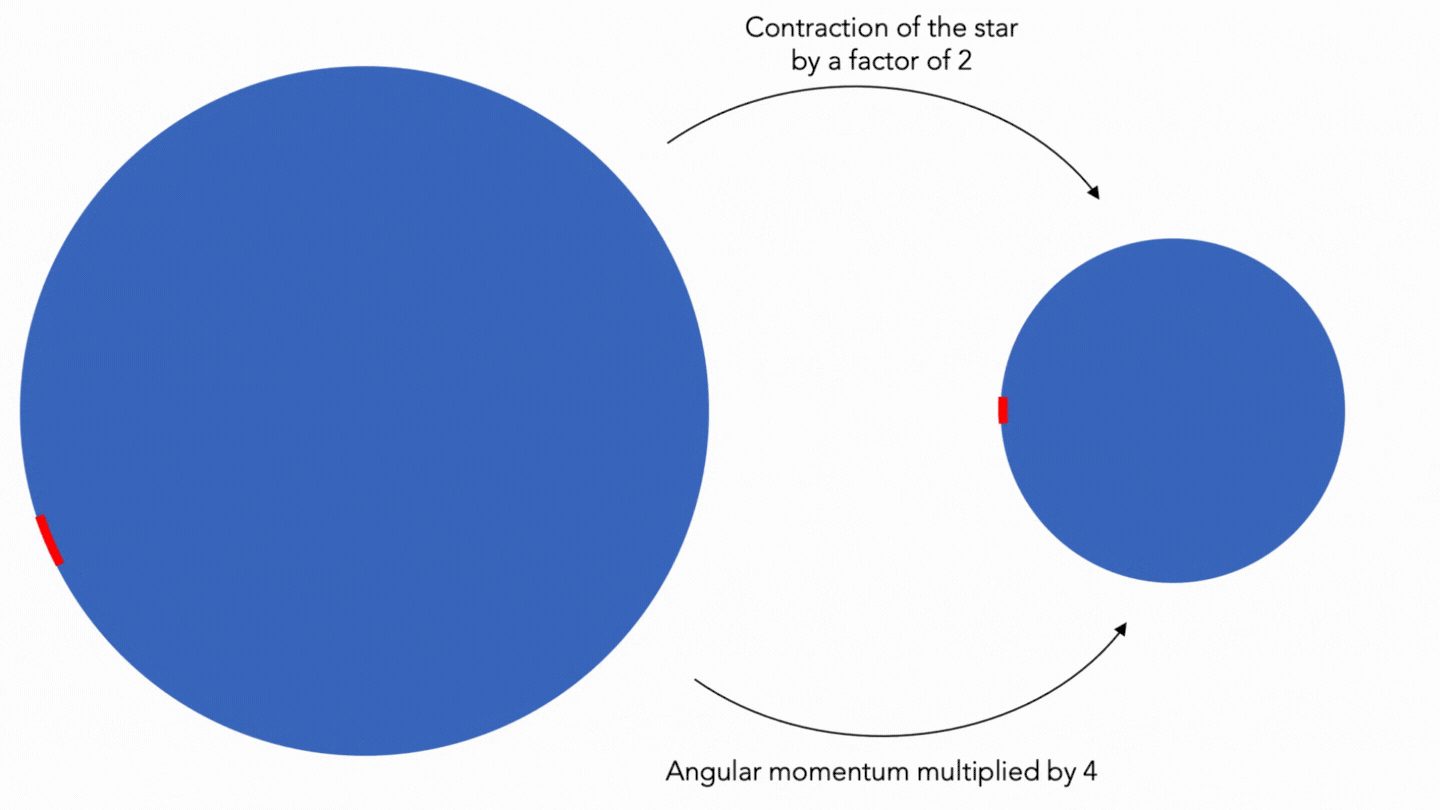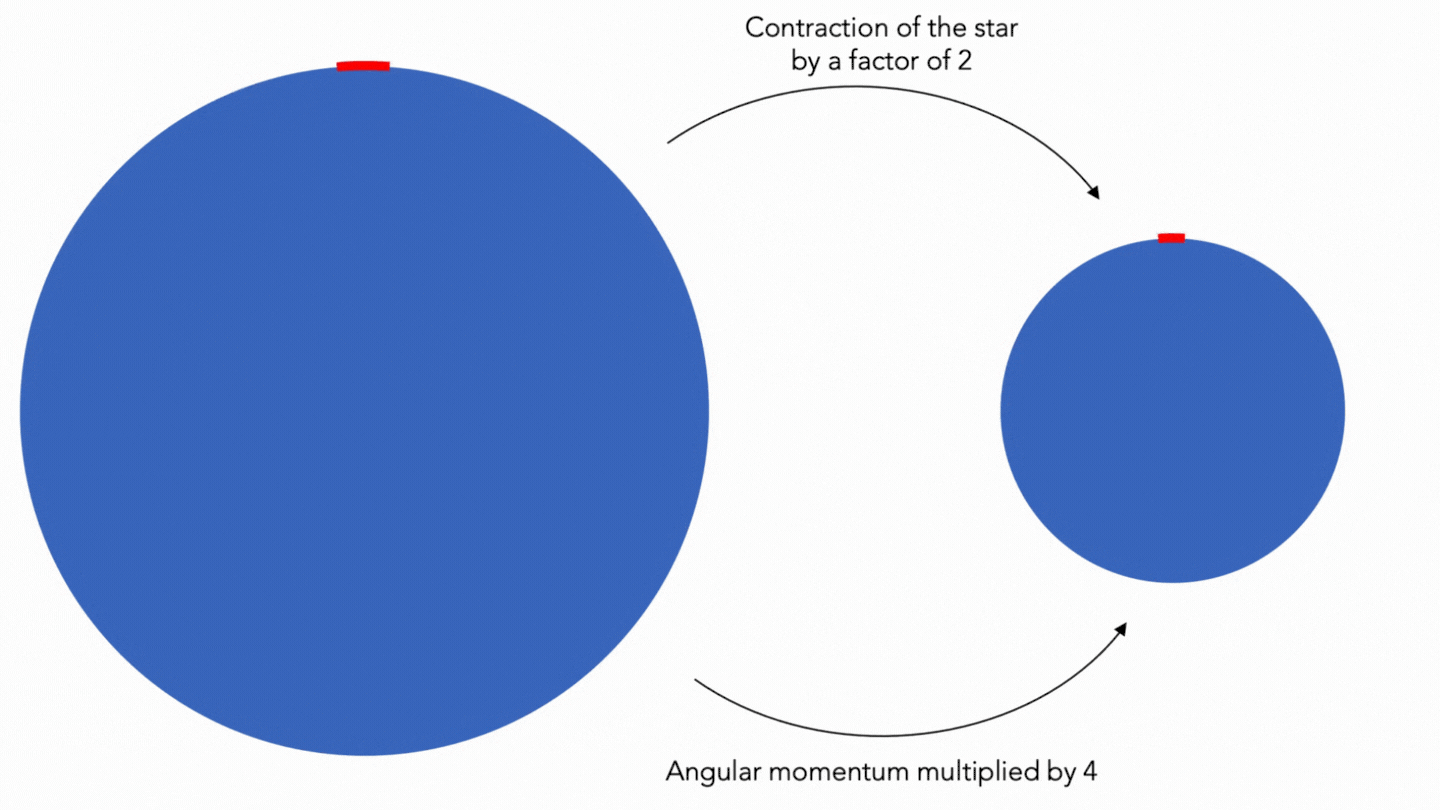© MH info Animation on the conservation of the angular momentum

Their magnetic field is also extremely intense (can reach up to 10¹⁴ T: they are then called magnetars): the Earth's magnetic field is 20 µT, and the most intense magnetic field generated on Earth is a few tens of teslas, enough to make objects levitate! The gravitational field would be so intense that the surface of neutron stars would be almost perfectly smooth. According to the latest computer simulations on neutron stars, a few 'mountains' could exist: their maximum size would be limited to a fraction of a millimetre! The causes of the formation of asperity like these can be linked to the accretion of matter. Neutron stars are thought to be composed of a crust, itself composed of free ions and electrons, as well as free neutrons and amazingly strange atomic nuclei, very rich in neutrons: nickel-62 (usually nickel-58), krypton-118 (usually krypton-83) or zinc-80 (usually zinc-64). These nuclei can actually proliferate due to the titanic pressure, which increases as we approach the centre. Neutron stars would be also composed of a core, defying the limits of current physics models. This core could be composed of a superfluid or a plasma of quarks and gluons, or baryons rather, unusual… made up of strange quarks, then forming hyperons! Finally, they would possess properties of superconductivity and superfluidity.

Superconductivity is characterised by an absence of electrical resistance. Superfluidity is a state of matter in which it behaves like a fluid with no viscosity, that is to say no resistance to movement: the movement of a superfluid produces no friction.

In July 1967, Jocelyn Bell-Burnell was a British student at Cambridge University studying quasars for her PhD thesis. While examining the records of a radio telescope (about 30 metres of paper to be analysed per day), she discovered a signal that was different from the usual signals, of improbable regularity and stability. When she announced this to Antony Hewish, her thesis supervisor, he rejected the observation, considering it to be the result of interference caused by a terrestrial instrument. Convinced that this was not the case, Jocelyn Bell continued her research. A few months later, Antony Hewish finally took an interest in the observation made by his student. The source of this signal was then suspected to be of artificial origin, and therefore extra-terrestrial. The body was therefore temporarily named LGM-1, for Little Green Men 1! In 1968, the results of Jocelyn Bell's, Antony Hewish's and his colleague’s research were published in the journal Nature: "Observation of a Rapidly Pulsating Radio Source, that seems to come from a neutron star or white dwarf", signed by Antony Hewish (first) and then Jocelyn Bell and three other colleagues (Observation of a Rapidly Pulsating Radio Source, 24^th February 1968, Nature). A neutron star − never observed at the time, but predicted by Walter Baade and Fritz Zwicky in 1934 − was indeed the source. Later, these sources of radio waves were called pulsars, for pulsating star. The pulsar discovered by Jocelyn Bell, CP 1919 (for Cambridge Pulsar), is now called PSR B1919+21 (for Pulsating Source of Radio) due to a unification of pulsar nomenclature. In 1974, Antony Hewish and Martin Ryle (an astronomer who developed radio telescope systems) were awarded the Nobel Prize in Physics 'for their pioneering research in radio astrophysics: Ryle for his observations and inventions, and Hewish for his decisive role in the discovery of pulsars'. Jocelyn Bell did not receive the Nobel Prize, which led to much controversy. However, she said that she "felt it was right that a Nobel Prize should be awarded to the supervisor and not to his student" and later received many awards. She is also known as the discoverer of pulsars.

Pulsars, neutron stars with a very high magnetic field and rotation speed, emit very strong electromagnetic radiation at their magnetic poles (like a magnet), taking the form of a jet. Indeed, the magnetic axis of stars is generally not aligned with their axis of rotation:

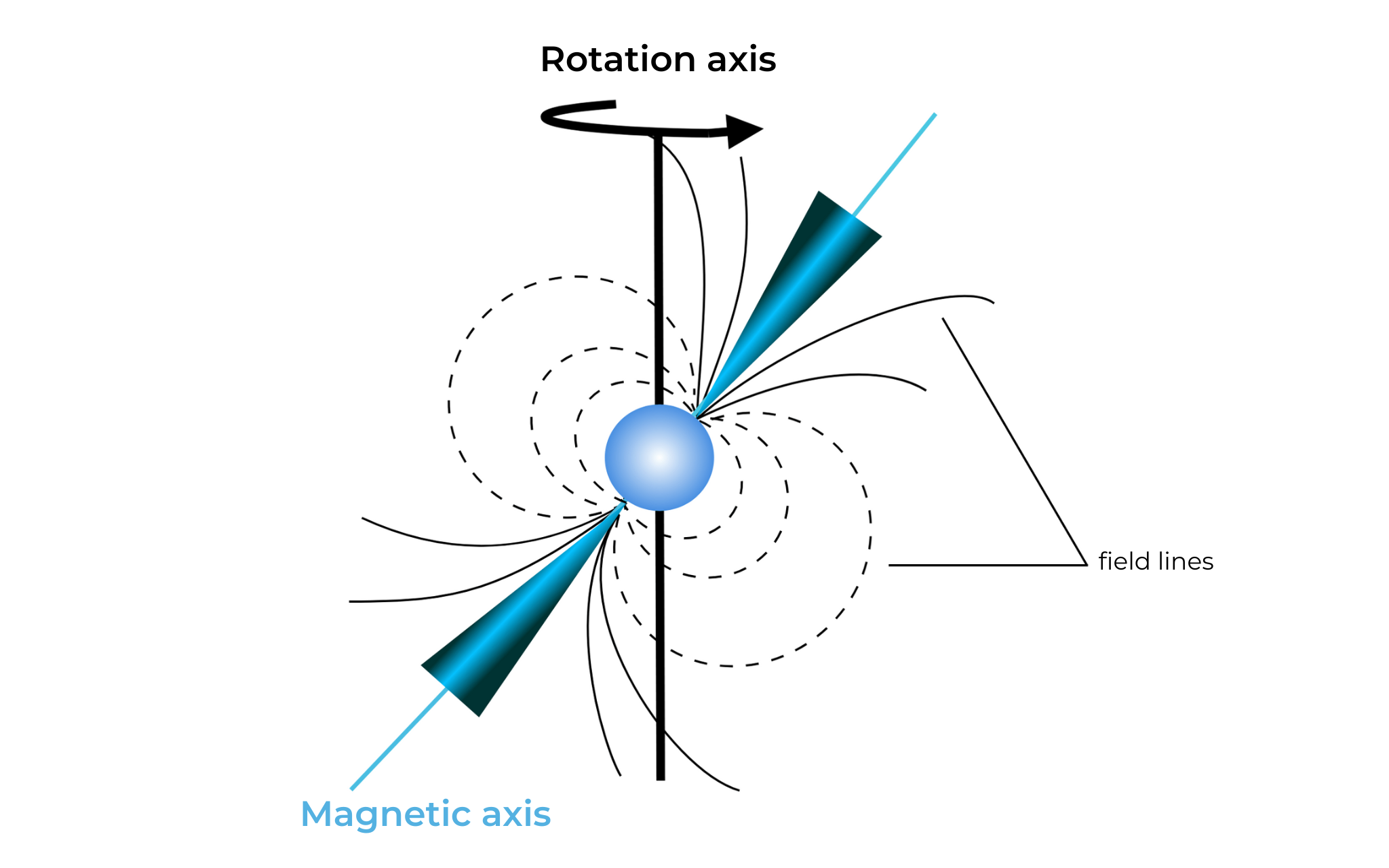© Undead Stars – Spaceboe © MH info Diagram of a pulsar

This produces large fluctuations in magnetic field strength (high-lowhigh-low...):

© Science Clic (Youtube) © MH info Fluctuation of the electromagnetic field strength for a given point

Logically, the closer the magnetic axis of these cosmic lighthouses is to perpendicular to the observer, the more intense the fluctuations will be. This gives the impression of a pulsating or flickering light − which can be observed hundreds of light years away from its source − as fluctuations in the intensity of the electromagnetic field produce fluctuations in the intensity of the emitted electromagnetic radiation. Radio pulsars represent the majority of pulsars discovered: these pulsars emit electromagnetic radiation in the radio wave range (usually very low frequency). They can thus be observed with radio telescopes. However, there are also optical (visible light), X (X-rays) and gamma (gamma rays) pulsars, which are rarer.

© Club Visuals (Youtube) © MH info View of a pulsar by an observer

On the other hand, the faster a pulsar rotates, the higher is the frequency of the fluctuations, the smaller is the wavelength of the emitted radiation. The rotation period of a pulsar is the time it takes for a pulsar to rotate on itself: it is therefore also the interval between two pulses. For example, for a pulsar with a period of 50 ms, an observer will see a light pulse every 50 milliseconds. The probability of observing a pulsar with a period of less than a millisecond (that is to say more than 1000 revolutions per second) is very low: in this case, it would generate gravitational waves, causing it to lose a lot of energy and thus slow down. The period during which it would be possible to observe pulsars with such speeds would therefore be extremely limited.

Stars between 7 and 10 M_☉ could, after evolving into a black dwarf, hypothetically evolve into a 'black supernova', after 10¹¹⁰⁰ years (advice: don't try to write it by hand! It would take more than half a page with this font and size), or 101,090 times the age of the Universe! This is thus the hypothetical evolution of a hypothetical evolution: so take it 'with a pinch of salt' ! Black dwarfs that could evolve into black supernovas would make between 7 and 10 M_☉ during their main sequence. This phenomenon would be possible through to called 'pycnonuclear' fusion (cold fusion): a single fusion of oxygen into silicon or silicon into iron would take millions of years!

Stars with a mass of more than 20 M_☉ (very massive stars):

Stars of more than 20 M_☉ will reach the temperature necessary for the fusion of carbon (6 x 10⁸ K) − and other fusion reactions of heavier elements, up to iron − before the core degenerates. Thus, the latter will then take on a structure called 'onion peel':

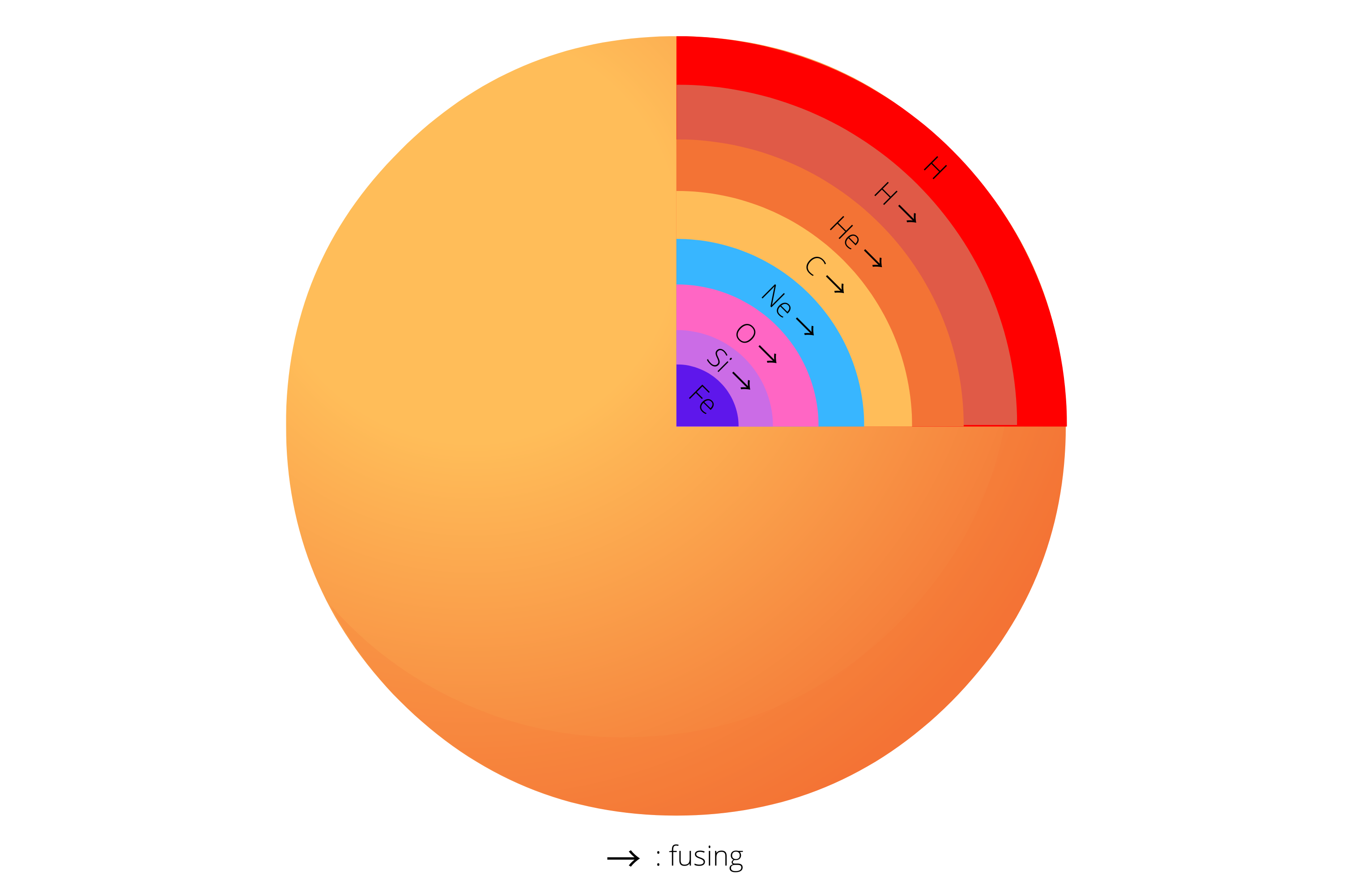Diagram of an onion peel star structure

The main elements produced by stellar nucleosynthesis (the term used in astrophysics to designate all the nuclear reactions occurring within stars) are those mentioned above and in the diagram, but also other elements, produced in smaller quantities: all the atoms present in the Universe (up to Iron) have been and are produced by calm nucleosynthesis. The synthesis of elements heavier than Iron is carried out by supernova nucleosynthesis. It is so called because of the gigantic production of energy in a very short period of time and occurs by neutronic capture (r and s processes), protonic capture (rp-process) or by photodisintegration (p-process). Nuclei very rich in protons or neutrons are then produced: this explains the majority of neutrons in uranium (92 protons for 147 neutrons), produced by the r process. However, unstable nuclei that are far too rich in protons or neutrons disintegrate soon after their formation, forming more stable nuclei that are still rich in neutrons. Furthermore, several processes can take place in the same nucleus.

After the fusion of carbon, many other fusions will take place: Neon, Oxygen, Silicon, Sulphur, Argon, Calcium, Titanium, Chromium... up to Iron (Sulphur, Argon, Calcium, Titanium, Chromium, and other elements − not present on the diagram above − are produced in more limited quantities). While hydrogen fusion takes a considerable amount of time, silicon fusion takes only a few weeks!

Iron being the most stable element, its fusion requires more energy than it produces (it is endothermic)! The iron core contracts abruptly and considerably. This constrains, as in the case of 8 to 20 M_☉ stars, some electrons to penetrate the atomic nuclei by fusing with protons, becoming neutrons. This fusion can also be called 𝜀 decay (epsilon) decay, it can also be considered a variant of \(\beta^+\) decay. The amount of neutrons also increases considerably (\( p^+ + e^- + \rightarrow n + \nu_e \)).

The core of the star becomes so dense that it can no longer be compressed, there is no space between the atoms: this one has a density of 10¹⁵ g/cm³. By way of comparison, osmium, the densest element on Earth, has a density of 22.587 g/cm³! The compression is therefore abruptly stopped again.

Only, the outer layers of the star do not compress at the same speed as the core because of their inertia. Inertia (or the principle of inertia) is the resistance that a body put up to a change in motion (setting in motion, stopping or changing speed). It varies according to mass, state of matter and density: body not very massive, in a solid state, and dense will have very low inertia, in contrary a massive body, gaseous and low-density will have very high inertia. The stopping wave propagates at a subsonic speed near the core, then, once it has passed, at a supersonic speed, producing a shock wave. The stopping wave can be compared to wagons connected to each other and to a (moving) locomotive by springs: if the locomotive stops, the last wagon does not stop immediately: one can imagine this as a stopping wave. It is also right to imagine the cars connected normally, but the effect would be almost imperceptible.

One might think that the shockwave would cause a supernova to expel the outer layers: yet the energy produced is only one hundredth of the energy required for a supernova to be bright and explode! Indeed, supernova explosions are still mysterious and should not exist according to our current models... Since they can be observed, this shows that, however beautiful the theories are, gaps are always inevitable.

After this impressive and mysterious explosion, a much stranger and more complex residue is found at the centre of the afterglow, exceeding the Oppenheimer-Volkoff limit, the maximum mass that a neutron star can have: beyond this limit, the star collapses on itself... into a black hole...